我们知道,通常的点分治方法都基于重心,删除重心后将每个连通块分别分治。正常情况下寻找重心需要做树DP,需要遍历两次树(即使从上一层传入点数,也得在上一层遍历一次),某些选手就用了一些黑科技:从上一层传入“本层中与上一层重心相连的点”(称为根,记作 $K$)的以“上一层的根”为根的子树大小作为本层总点数。
听起来很拗口,实际上是这么回事:(图中 $K'$ 表示本层的根,$K$ 表示上一层的根)
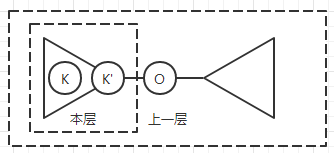
可以明显发现,当 $K$ 和 $K'$ 处于上一层重心 $O$ 的同一子树时,传入的点数是错误的。
这是否会对时间复杂度造成影响呢?
这与找重心的方式有关。我们讨论两种最常见的找法:
法1
从本层的根开始深度优先遍历,并同时计算出子树大小,以第一个所有子树大小不超过 $\frac{n}{2}$ 的为重心。
结论:算法错误
设传入的点数值为 $n$。
可以举出反例:考虑这样一棵树:由重心和端点与之相连的三条长 $\frac{n-1}{3}$ 的链组成。初始的根位于某个叶子处。
第一层分治,传入到根所在链的大小为 $\frac{2n+4}{3}\geq 2\cdot\frac{n-1}{3}$,因而任何点都符合条件。按照深度优先顺序,这次找的“重心”是第一层的根。
第二层分治,传入到根所在链的大小为 $2<\frac{1}{2}\cdot(\frac{n-1}{3}-1)$(当 $n\geq 16$ 时)。这时不存在符合条件的点,分治无法进行,算法错误。
法2
从本层的根开始深度优先遍历,并同时计算出子树大小,将传入值与以自身为根子树大小之差作为向本层根方向的子树大小,再取最大子树最小的点为重心。
结论:算法正确,递归层数 $O(\log n)$,访问节点的总次数 $O(n\log n)$。
我们来分析时间复杂度:
我们将分治结构稍作改变,只考虑输入点数等于实际点数的问题。显然当点数为 $1$ 时访问节点数 $O(1)$。
初始问题是符合条件的。现在考虑把问题分解前处理一层产生的代价(包括递归但大小错误的部分):
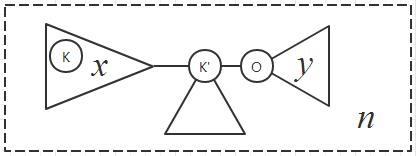
由于只有本层的根所在的方向递归时会错误,因而只要考虑对于本层重心而言根所在子树即可。
考虑一个问题。设本层实际大小为 $n$,以 $O_1$ 为根时含 $K_1$ 子树的根为 $K_1'$(也有可能 $O_1=K_1$,这时没有出现错误,复杂度正确),以 $K_1$ 为根时子树 $O_1$ 的大小为 $y_1$,以 $K_1'$ 为根时 $K_1$ 所在子树大小为 $x_1$。(均指实际大小)
解决本层的访问节点数为 $O(n)$。现在考虑递归到 $K'$ 的错误部分。该部分的实际点数为 $n-y_1$,传入点数为 $n-x_1$。设该部分处理时与上一层对应的部分用层数下标表示。以此类推直到 $K_i=O_i$ 为止。这一系列问题访问的总点数即为问题处理的代价。
运用归纳法,我们可以知道每一次的实际点数 $N_i$ 分别为 $n,n-y_1,n-y_1-y_2,...,n-\sum_{i=1}^{n-1}y_i$,传入点数 $N'_i$ 分别为 $n,n-y_1,n-x_1-y_2,...,n-\sum_{i=1}^{n-2}x_i-y_{i-1}$。
下面证明 $x_i \leq y_i$。使用归纳法,设对于 $j < i$ 该结论均成立(由重心显然对于第 $1$ 层成立)。实际上,若 $x_i > y_i$ 则对“重心”$O_i$ 而言包含 $K_i$ 的子树为最大子树,并且由于 $x_{i-1} \leq y_{i-1}$,本层的传入点数不小于实际点数。这样,用传入点数减去子树大小算出的点数不小于 $x_i$。故该算法计算出的 $O$ 的最大子树必为 $K_i'$ 且计算出的大小不小于 $x_i$。对 $K_i'$ 而言,除 $O_i$ 外的各子树大小计算值均小于其作为 $O_i$ 子树的计算值。又 $y_i< x_i$,故子树 $O_i$ 也小于该值。这样 $K_i'$ 计算出的最大子树严格小于 $O_i$ 的,与重心的计算定义矛盾。
更进一步地,我们可以证明 $y_i\geq \frac{1}{2}N_i$。证明方法类似:假设 $y_i<\frac{1}{2}N_i$,同上可证其最大子树必为 $K_i'$ 且计算的大小不小于其实际值,$N_i-y_i > y_i$。则对于 $K_i$ 而言,也可以用类似上一段的方法证明其计算出的最大子树严格小于 $O_i$,与重心的计算定义矛盾。
故有 $N_{i+1}\leq \frac{1}{2}N_i$。由于第 $i$ 层的访问点数为 $O(N_i)$,一个规模为 $n$ 的问题处理总点数满足 $T(n)=T(\frac{n}{2})+O(n)$,解得 $T(n)=O(n)$,且这部分递归层数 $O(\log n)$。
故分治时处理一个问题的时间为 $O(n)$。并且其分解出的子问题互不相交且都是正确方法的某个子问题的子集,故递归层数和子问题的时间复杂度不高于一般点分治。证毕。

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号